Chan group

Nonlinear mode coupling and fluctuation induced transitions

in electromechanical resonators

 

 

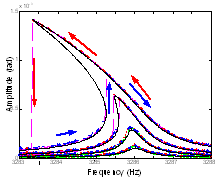
Under sufficiently large periodic drive, nonlinear oscillators develop multistability and exhibit hysteresis in their frequency response. The presence of fluctuations enable the system to occasionally overcome the activation barrier and switch between the coexisting states. Unlike systems in thermal equilbrium, these oscillators are driven far from equilibrium and cannot be characterized by free energy. They possess certain properties that have no analog in equilibrium systems. Apart from fundamental interests, the sharp jump in the oscillation amplitude or phase at a bifurcation point could be used for enhancing detection sensitivity.

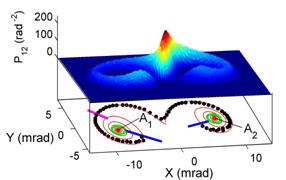
Switchings in the driven nonlinear oscillators take place in a two-dimensional phase space. Even though switching occurs randomly in time, in phase space the system follows trajectories concentrated around the "most probable switching path".  With our theory collaborators, we demonstrate the breaking of time reversal symmetry in switching of systems far from thermal equilibrium.

We also have observed a number of generic features for switching. For instance, we measured two different scaling of the activation barrier close to the bifurcation points. When the oscillator is resonantly driven into bistability, the activation barrier varies with frequency detuning with critical exponent of 3/2, consistent with predicted universal scaling relationships for saddle node bifurcations. When the oscillator is driven into parametric resonance, the critical exponent becomes 2 as a different kind of bifurcation is involved.

 

Coupled parametric oscillators: From disorder-induced current to asymmetric Ising model

C. Han, M. Wang, B. Zhang, M. I. Dykman, and H. B. Chan

Phys. Rev. Research 6, 023162(2024). pdf

 

Energy Transfer into Period-Tripled States in Coupled Electromechanical Modes at Internal Resonance

Yingming Yan, X. Dong, L. Huang, K. Moskovtsev and H. B. Chan

Phys. Rev. X 12, 031003 (2022). pdf

 

Frequency stabilization and noise-induced spectral narrowing in resonators with zero dispersion

L. Huang, S. M. Soskin, I. A. Khovanov, R. Mannella, K. Ninios and H. B. Chan

Nature Communications 10, 3930 (2019). pdf

 

Strong negative nonlinear friction from induced two-phonon processes in vibrational systems

X. Dong, M. I. Dykman and H. B. Chan

Nature Communications 9, 3241 (2018). pdf

 

Correlated anomalous phase diffusion of coupled phononic modes in a sideband-driven resonator

F. Sun, X. Dong, J. Zou, M. I. Dykman and H. B. Chan

Nature Communications 7, 12694 (2016). pdf

 

Telegraph frequency noise in electromechanical resonators

F. Sun, J. Zou, Z. A. Maizelis and H. B. Chan

Physical Review B  91, 174102 (2015). pdf

 

Work fluctuations in a nonlinear micromechanical oscillator driven far from thermal equilibrium

P. Zhou, X. Dong, C. Stambaugh and H. B. Chan

Physical Review E  91, 052110 (2015). pdf

 

Poisson noise induced switching in driven micromechanical resonators

J. Zou, S. Buvaev, M. Dykman and H. B. Chan

Physical Review Letters B 86, 155420 (2012). pdf

 

Activation barrier scaling for fluctuation induced switching in driven non-linear micromechanical oscillators

 H. B. Chan and C. Stambaugh

Journal of Statistical Mechanics: Theory and Experiment,  P01028 (2009). pdf

 

Switching-path distribution in multidimensional systems

H. B. Chan, M. I. Dykman and C. Stambaugh

Physical Review E 78, 051109 (2008). pdf

 

Paths of fluctuational induced switching

H. B. Chan, M. I. Dykman and C. Stambaugh

Physical Review Letters  100, 130602 (2008). pdf

 

Activation barrier scaling and crossover for noise-induced switching micromechanical parametric oscillators

H. B. Chan and C. Stambaugh

Physical Review Letters  99, 060601 (2007). pdf

 

Supernarrow spectral peaks near a kinetic phase transition in a driven, nonlinear micromechanical oscillator

C. Stambaugh and H. B. Chan

Physical Review Letters  97, 110602 (2006). pdf

 

Fluctuation-enhanced frequency mixing in a nonlinear micromechanical oscillator

H. B. Chan and C. Stambaugh

Physical Review B 73, 224301 (2006). pdf

 

Noise activated switching in a driven, nonlinear micromechanical oscillator

C. Stambaugh and H. B. Chan

Physical Review B 73, 172302 (2006). pdf